Quantum Radar
Quantum Radar
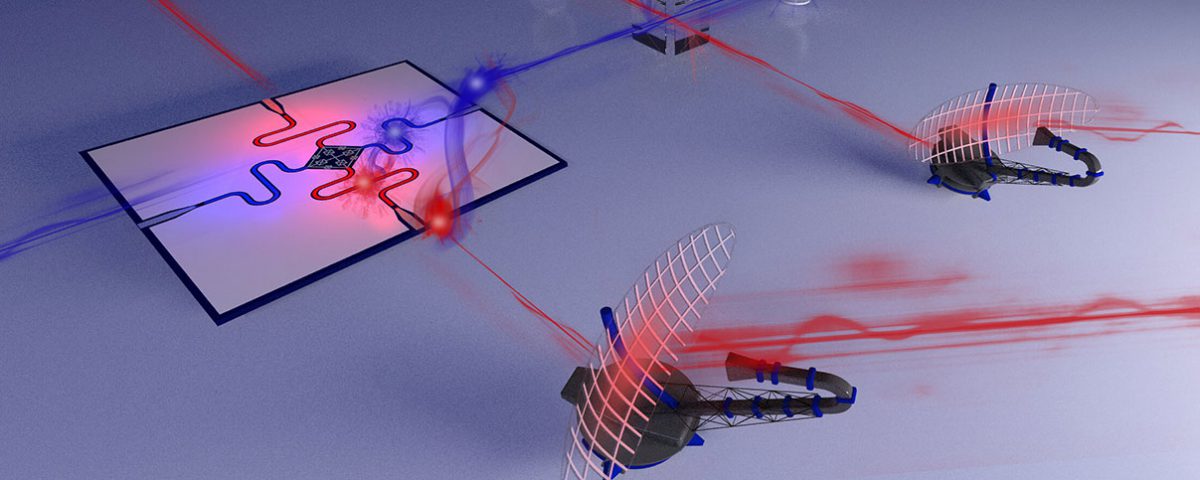
Quantum Radar: fundamentals and basic working principle
The working principle of a Quantum Radar (QR) is based on the principle of Quantum Illumination (QI) which in turn has at its heart the phenomenon of Quantum Entanglement of continuous variables. Similar to the discrete case, variables having continuum outcomes may as well be entangled. For example, the electric field components of light of different wavenumbers (k) or frequency (ω) may be entangled to one another when there is a possibility of them mutually interacting. Together they form a larger composite system where the individual sub-systems will have correlations. Light fields are denoted by Bose field operators (ˆb, ˆb † ) which obey the following commutation relation [ ˆbj , ˆb † k ] = δjk. Complex combinations of these operators can give rise to position or momentum like continuous observables. Namely

Where ~ is the Planck’s constant.
ENTANGLEMENT OF CONTINUOUS OBSERVABLES
Two observables 1,2 with a discrete set of measurement outcomes say {a, b} will be in an entangled state given by
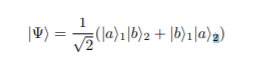
Consider two quantum systems with position and momentum operators (ˆx1, xˆ2, pˆ1, pˆ2). One can now define the following two observables Xˆ+ = (ˆx1 + ˆx2) and Pˆ− = (ˆp1 − pˆ2) 1 . They are maximally entangled if their total variance obtained with respect to some density operator ρ is equal to zero.

Where hΘˆ iρ = T r[ρΘ].
THE WORKING PRINCIPLE OF THE QUANTUM RADAR
The QR consists of an emitter and a receiver. Each of these units comprises of two electromagnetic resonators. On one side is a superconducting microwave cavity (MC) operating at frequency ωw. While on the other side there is an optical cavity (OC) operating at frequency ωo. The two are capacitively connected by a mechanical resonator (MR) to drive the OC. The MR is optically coated on the OC side to serve as a micro-mirror for the optical Fabry-Perot cavity. Each of these oscillators have their own fields, the OC and the MC fields are denoted by (ˆao, aˆ † o ) and (ˆaw, aˆ † w). respectively and the phonon fields of the MR are denoted by (ˆb, ˆb † ) with frequency ωM. The number operators for the respective fields are Nˆ o = ˆa † oaˆo, Nˆw = ˆa † waˆw and NˆM = ˆb †ˆb. The system is externally driven by the microwave and the optical fields, which is a harmonic perturbation operating at frequency ωd,j , j = o, w. The perturbing part of the Hamiltonian is denoted by Hˆ d(ωd,j ). With this the Hamiltonian for the entire system will be

FIG. 1: Working principle of a quantum radar. The top converter couples two entangled beams, a microwave one (red wavy line) and a visible one (red straight line). The microwave reflection is converted to visible light that interferes with the initial visible beam in the detector.

Where ∆0,j = ωj − ωd,j is the detuning from the resonant frequencies ωj . In the limit of weak optomechanical coupling (gj → 0), one can expand the operators ˆaj , aˆ † j about their steady-state field amplitudes. The steady-state is characterized by mean photon number (intensity) in the cavity hNˆ j i = Nj 1. Therefore the mean amplitude is proportional to p Nj . Hence the fluctuations in the fields ˆaj about the steady state value is ˆcj ≡ aˆj − p Nj . In the Interaction picture where all the electromagnetic fields are expressed in terms of the ˆcj , cˆ † j operators and furthermore neglecting the high frequency effects pertaining to ‘±2ωM’, the above Hamiltonian will assume the following form
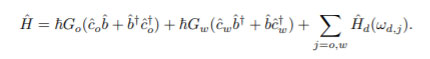
Where the Gj = gj p Nj is the multi-photon couplings. Now to understand the Microwave-Optical entanglement, one must be able to relate the outgoing electromagnetic waves with the intra-cavity electromagnetic excitations. To achieve this, the following operators for the outgoing microwave ( ˆdw) and optical ( ˆdo) fields are defined, in terms of (ˆcw, cˆ † w, cˆo, cˆ † o ).

Where Aw,o, B are complex coefficients accounting for the co-operative effects inside the cavity. Of primary interest are the following quantities
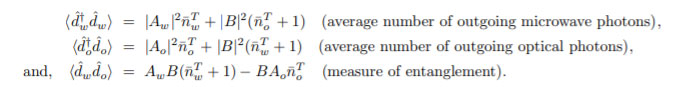
Where ¯n T j = 1 e ~ωj /kBT +1 is the Planck distribution function at absolute temperature ‘T’ and kB is the Boltzmann constant. The last among the three equations in Eq.(8) accounts for the entanglement among ˆdw and ˆdo. The outgoing microwave and the optical fields will be entangled if and only if

N.B. Eq.(7) does not have the Brownian noise operators. One may easily include them and obtain the equivalent expressions in Eq.(8).
